拓扑排序
什么是拓扑排序
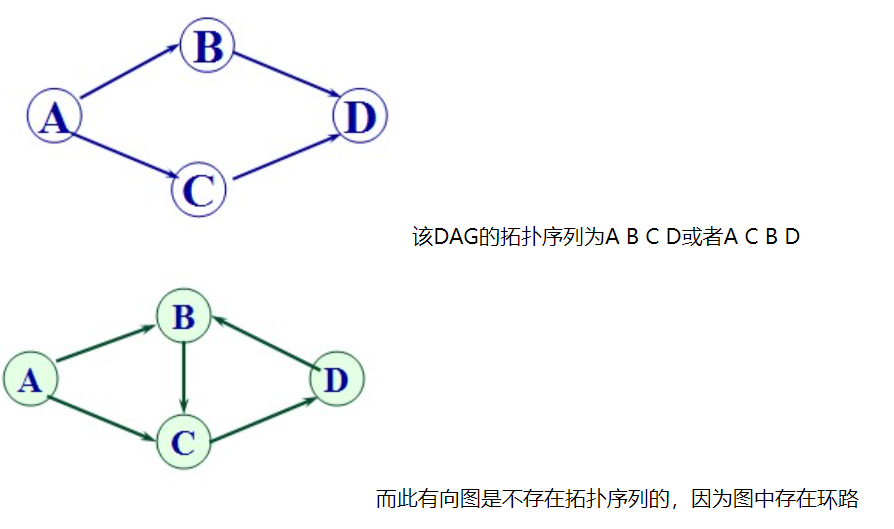
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若<u,v> ∈E(G),则u在线性序列中出现在v之前。
通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。
注意:
1)只有有向无环图才存在拓扑序列;
2)对于一个DAG,可能存在多个拓扑序列;
来源: https://www.cnblogs.com/dolphin0520/archive/2011/04/16/2017737.html
直观点说, 就是把一幅图拉平, 而这个拉平的图里, 所有的箭头方向是一致的(即不改变原序列顺序), 如下图所示:
相关例题
207-课程表: https://leetcode-cn.com/problems/course-schedule/
判断有向图是否存在环
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 1050 <= prerequisites.length <= 5000prerequisites[i].length == 20 <= ai, bi < numCoursesprerequisites[i]中的所有课程对 互不相同
解法: 将问题转化为有向图这种数据结构, 只要图中存在环, 那就说明存在循环依赖, 肯定没办法全部上玩课程.
图的结构: 邻接表
List<Integer>[] graph;
graph[s] 是一个列表,存储着节点 s 所指向的节点。
建图函数:
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int to = edge[0];
int from = edge[1];
graph[from].add(to);
}
return graph;
}
如何判断图中有没有环?
- 先得会遍历
- 在遍历中寻找环
DFS遍历框架:
// 防止重复遍历同一个节点
boolean[] visited;
// 从节点 s 开始 DFS 遍历,将遍历过的节点标记为 true
void traverse(List<Integer>[] graph, int s) {
if (visited[s]) {
return;
}
/* 前序遍历代码位置 */
// 将当前节点标记为已遍历
visited[s] = true;
for (int t : graph[s]) {
traverse(graph, t);
}
/* 后序遍历代码位置 */
}
修改后的DFS遍历代码:
// 从节点s开始DFS遍历, 将遍历过的结点标记为true.
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
visited[s] = true;
onPath[s] = true;
for(int t : graph[s]) {
traverse(graph, t);
}
onPath[s] = false;
}
完整代码
import java.util.LinkedList;
import java.util.List;
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
boolean[] onPath;
boolean[] visited;
boolean hasCycle = false;
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
traverse(graph, i);
}
return !hasCycle;
}
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int to = edge[0];
int from = edge[1];
graph[from].add(to);
}
return graph;
}
// 从节点s开始DFS遍历, 将遍历过的结点标记为true.
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
visited[s] = true;
onPath[s] = true;
for(int t : graph[s]) {
traverse(graph, t);
}
onPath[s] = false;
}
}
//leetcode submit region end(Prohibit modification and deletion)
例题
210-课程表II : https://leetcode-cn.com/problems/course-schedule-ii/
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= numCourses * (numCourses - 1)prerequisites[i].length == 20 <= ai, bi < numCoursesai != bi- 所有
[ai, bi]互不相同
解法:
如果把课程抽象成节点, 课程之间的依赖关系抽象成有向边, 那么这幅图的拓扑排序结果就是上课顺序.
完整代码:
import java.util.*;
//leetcode submit region begin(Prohibit modification and deletion)
class Solution {
//List<Integer> preorder = new ArrayList<>();
List<Integer> postorder = new ArrayList<>();
boolean[] onPath;
boolean[] visited;
boolean hasCycle = false;
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
visited = new boolean[numCourses];
onPath = new boolean[numCourses];
for (int i = 0; i < numCourses; i++) {
traverse(graph, i);
}
if (hasCycle) {
return new int[]{};
}
// 逆后序遍历结果即为拓扑排序结果
Collections.reverse(postorder);
int[] res = new int[numCourses];
for (int i = 0; i < numCourses; i++) {
//res[i] = preorder.get(i);
res[i] = postorder.get(i);
}
return res;
}
void traverse(List<Integer>[] graph, int s) {
if (onPath[s]) {
hasCycle = true;
}
if (visited[s] || hasCycle) {
return;
}
onPath[s] = true;
visited[s] = true;
//preorder.add(s);
for (int t : graph[s]) {
traverse(graph, t);
}
postorder.add(s);
onPath[s] = false;
}
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
List<Integer>[] graph = new LinkedList[numCourses];
for (int i = 0; i < numCourses; i++) {
graph[i] = new LinkedList<>();
}
for (int[] edge : prerequisites) {
int from = edge[1];
int to = edge[0];
graph[from].add(to);
}
return graph;
}
}
//leetcode submit region end(Prohibit modification and deletion)
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 jungle8884@163.com